Blog realizado como forma de avaliação da matéria de matemática na III unidade, pelo professor Matheus Souza de Oliveira.
INTRODUÇÃO A LÓGICA.
Proposições.
As proposições são palavras ou símbolos que expressam um pensamento, essas afirmações assumem valores lógicos que podem ser verdadeiros ou falsos e para representar uma proposição utilizamos as letras p e q.
exemplos de proposições:
O gato tem pelos;
O cachorro é veloz;
Todas as pessoas são mortais.
Conectivos.
As proposições simples, que já foram compostas, são ligadas por elementos que são chamados de conectivos.
Na proposição "O céu é azul e as nuvens são brancas" o elemento e é um conectivo que une duas proposições, já na proposição "O céu não é azul" o conectivo não modifica a proposição.
Tabela verdade.
Quando temos proposições compostas, os valores lógicos resultante dependem exclusivamente dos valores de cada proposição simples.
Diante disso, utilizamos um dispositivo chamado tabela verdade ou tabela de verdade, onde são colocados os valores de cada proposição e de acordo com os conectivos presentes ao valor lógico final.
A conjunção é utilizada quando entre as proposições existe o conectivo. Esta operação será verdadeira quando todas as proposições forem verdadeiras.
O símbolo utilizado para representar essa operação é o ^, colocado entre as proposições. Desta forma, quando temos p ^ q, significa "p e q".
INTRODUÇÃO A TEORIA DOS CONJUNTOS.
A teoria dos conjuntos é a teoria matemática capaz de agrupar elementos.
Dessa forma, os elementos (que podem ser qualquer coisa: números, pessoas, frutas) são indicados por letra minúscula e definidos como um dos componentes do conjunto.
A teoria dos conjuntos é a teoria matemática capaz de agrupar elementos. Dessa forma, os elementos (que podem ser qualquer coisa: números, pessoas, frutas) são indicados por letra minúscula e definidos como um dos componentes do conjunto.
Relação de Pertinência.
A relação de pertinência é um conceito muito importante na "Teoria dos Conjuntos".
Ela indica se o elemento pertence (e) ou não pertence (ɇ) ao determinado conjunto, por exemplo:
D = {w,x,y,z}
w e D (w pertence ao conjunto D)
j ɇ D (j não pertence ao conjunto D).
Relação de Inclusão.
A relação de inclusão aponta se tal conjunto está contido (C), não está contido (Ȼ) ou se um conjunto contém o outro (Ɔ), por exemplo:
A = {a,e,i,o,u}
B = {a,e,i,o,u,m,n,o}
C = {p,q,r,s,t}
A C B (A está contido em B, ou seja, todos os elementos de A estão em B)
C Ȼ B (C não está contido em B, na medida em que os elementos dos conjuntos são diferentes)
B Ɔ A (B contém A, donde os elementos de A estão em B).
Conjunto Vazio.
O conjunto vazio é o conjunto em que não há elementos; é representado por duas chaves {} ou pelo símbolo Ø. Note que o conjunto vazio está contido (C) em todos os conjuntos.
União.
A união dos conjuntos, representada pela letra (U), corresponde a união dos elementos de dois conjuntos, por exemplo:
A = {a,e,i,o,u}
B = {1,2,3,4}
AB = {a,e,i,o,u,1,2,3,4}.
CONJUNTOS NUMÉRICOS.
Na matemática os conjuntos numéricos que representam a classe dos números são representados por 5 (cinco) grandes conjuntos: Reais, Naturais, Irracionais, Racionais e Inteiros.
Conjunto dos números naturais (N).
O conjunto dos números naturais é representado pela letra N, contendo os números positivos incluindo o 0 (zero).
N = {0, 1, 2, 3, 4, 5, …}
É um conjunto infinito, não dá para representar todos os números, assim as reticências (…) indica que é um conjunto infinito. Também pode ser representado da seguinte forma:
N = {x ∈ N | x ≥ 0 }
Conjunto dos números inteiros (Z).
O conjunto dos números inteiros é representado pela letra Z, contendo todos os números naturais e os números negativos, que são os números opostos aos positivos.
Z = {…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…}
Também é um conjunto infinito nas duas extremidades.
Conjuntos dos números racionais (Q).
O conjunto dos números racionais é representado pela letra Q, contendo os números inteiros, forma decimal exata, os números na forma periódica ou na forma de fração.
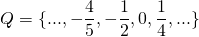
É um conjunto infinito também.
Números decimais na forma exata: Ex. {2,2; 5,432; 23,00009}
Números decimais na forma periódica: Ex. {3,2222…; 12,11111…; 40,12121212…}
Conjuntos dos números irracionais (I).
O conjunto dos números irracionais é representado pela letra I, contendo todos os números decimais não exatos e não periódicos.
Exemplos: 4,21315… ou 5,122030…
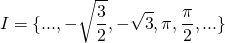
É um conjunto infinito.
Intervalos numéricos.
Uma maneira de representar conjuntos numéricos na matemática é através dos intervalos numéricos. É importante lembrar que só é possível representar intervalos numéricos para os conjuntos e subconjuntos do conjunto dos números reais.
Veja a seguir os tipos de intervalos:
Intervalo com extremos abertos
]a,b[ = {x ∈ R│a < x < b}

Intervalo com extremos fechados
[a,b] = {x ∈ R│a ≤ x ≤ b}

Intervalo aberto à direita e fechado à esquerda
[a,b[ = {x ∈ R│a ≤ x < b}

Intervalo aberto à esquerda e fechado à direita
]a,b] = {x ∈ R│a < x ≤ b}

INTRODUÇÃO A FUNÇÃO.
Na função constante, todo valor do domínio (x) tem a mesma imagem (y).
Fórmula geral da função constante:
f(x) = c
x = Domínio
f(x) = Imagem
c = constante, que pode ser qualquer número do conjunto dos reais.
Exemplo de gráfico da função constante: f(x) = 2
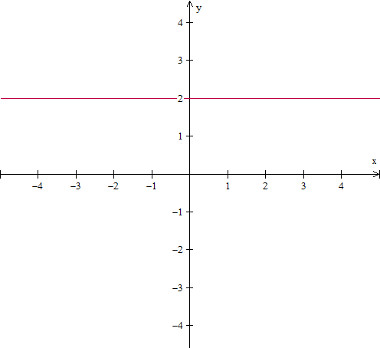
Fução injetora ou injetiva.
Nessa função, cada elemento do domínio (x) associa-se a um único elemento da imagem f(x). Todavia, podem existir elementos do contradomínio que não são imagem. Quando isso acontece, dizemos que o contradomínio e imagem são diferentes. Veja um exemplo:Conjunto dos elementos do domínio da função:
D(f) = {-1,5, +2, +8}Conjunto dos elementos da imagem da função:
Im(f) = {A, C, D}Conjunto dos elementos do contradomínio da função:
CD(f) = {A, B, C, D}
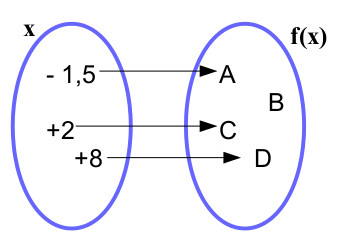
Domínio, imagem e contradomínio.

Matemática da Idade Contemporânea
Com a Revolução Industrial, a matemática se desenvolveu de forma extraordinária.
As indústrias e as universidades se tornaram um vasto campo para o estudo de novos teoremas e invenções de todo tipo.
Na álgebra, os matemáticos se debruçaram no desenvolvimento de resolução de equações, quatérnios, grupos de permutações e grupo abstrato.
Já no século XX, as teorias de Albert Einstein reformularam o que se entendia como Física. Deste modo, os matemáticos viram-se diante de novos desafios para expressar em número as ideias do genial cientista.
A teoria da relatividade supôs uma nova perspectiva sobre a compreensão do espaço, do tempo e mesmo do ser humano.





Nenhum comentário:
Postar um comentário