Blog realizado como forma de avaliação da matéria de matemática da III unidade, pelo professor Matheus de Souza Oliveira.
FUNÇÃO AFIM.
Uma função
Onde:
- a é o coeficiente angular do gráfico de f
- b é o coeficiente linear, ou o ponto de intersecção com o eixo y
- x é a variável independente.
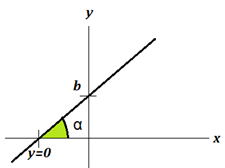
Podemos determinar o valor de a pela tangente do ângulo
Basicamente, o gráfico de uma função afim será sempre uma reta. Os fatores que vão determinar a sua posição no plano são os coeficientes linear e angular, particulares de cada função. Vamos apresentar alguns problemas que envolvem funções afim:
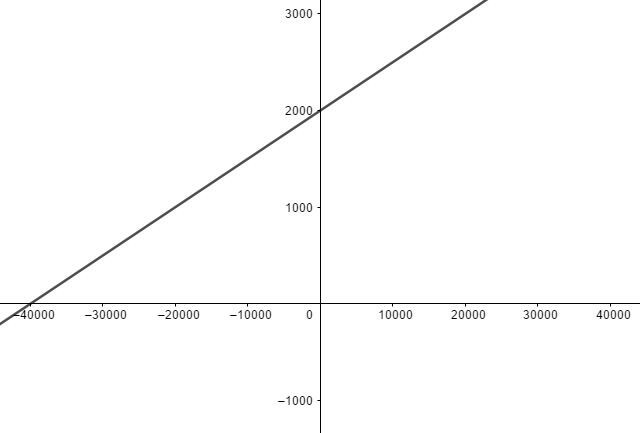
Exemplo, Supondo que você é um vendedor, cujo salário mensal é de R$ 2.000,00. Porém, a cada produto vendido você ganha uma comissão de 5%, ou 0,05 vezes o valor do produto. A função que descreverá, em função do valor vendido durante o mês é do tipo afim, e será descrita pela lei:
f(x) = 0,05x + 2000
FUNÇÃO INDENTIDADE.
Seja uma função
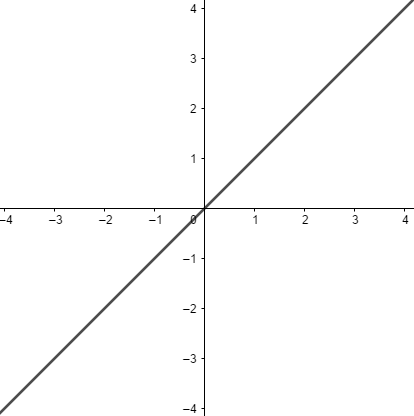
Uma função
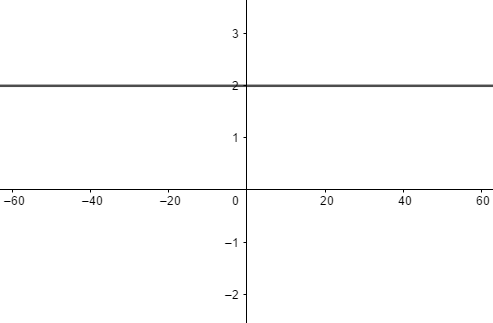
Por exemplo, seja a função f(x) = 2, o seu gráfico será:
FUNÇÃO LINEAR.
Uma função
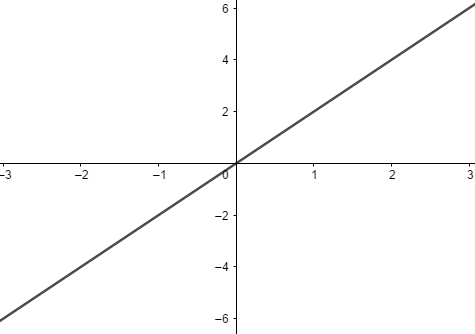
EXEMPLO DE FUNÇÃO LINEAR.
f(x) = – 2x
Essa também é uma função linear, pois seus coeficientes são a = – 2 e b = 0. Podemos ainda dizer que essa função é decrescente, uma vez que a < 0.
TRANSLAÇÃO DA FUNÇÃO INDENTIDADE.
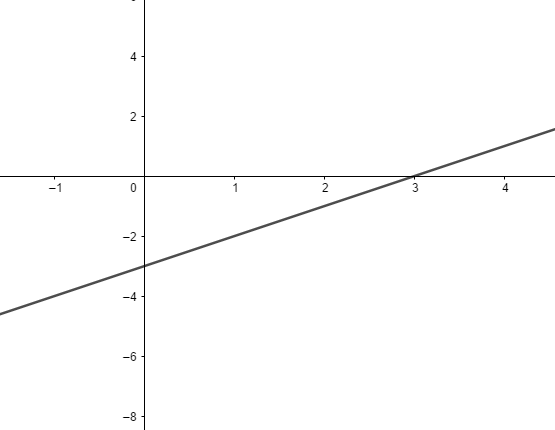
Se tomarmos a função identidade e acrescentarmos à ela um coeficiente linear e mantendo o seu coeficiente angular igual a 1, ocorrerá a translação da reta. A função será definida por f(x) = x+b sendo a = 1 e
FUNÇAO POLINOMINAL DO 1º GRAU.
Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a![]() 0.
0.
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
GRÁFICO.
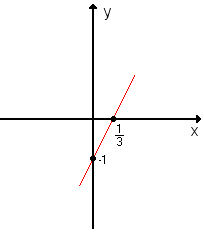
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a![]() 0, é uma reta oblíqua aos eixos Ox e Oy. Por exemplo, vamos construir o gráfico da função y = 3x - 1:
0, é uma reta oblíqua aos eixos Ox e Oy. Por exemplo, vamos construir o gráfico da função y = 3x - 1:
Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
a) Para x = 0, temos y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1)..
b) Para y = 0, temos 0 = 3x - 1; portanto, ![]() e outro ponto é
e outro ponto é ![]()
Marcamos os pontos (0, -1) e ![]() no plano cartesiano e ligamos os dois com uma reta.
no plano cartesiano e ligamos os dois com uma reta.
| x | y |
| 0 | -1 |
| 0 |
Já vimos que o gráfico da função afim y = ax + b é uma reta.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, está ligado à inclinação da reta em relação ao eixo Ox.
O termo constante, b, é chamado coeficiente linear da reta. Para x = 0, temos y = a · 0 + b = b. Assim, o coeficiente linear é a ordenada do ponto em que a reta corta o eixo Oy.
FUNÇÃO QUADRÁTICA.
Uma função quadrática é uma função da forma f(x) = a x2 + b x + conde a, b e c são números reais a 0.
O GRÁFICO DA FUNÇÃO QUADRÁTICA.
Entre as equações quadráticas a mais simples é f(x) = x2. O seu gráfico servirá como base para construirmos os gráficos de outras equações quadráticas.
Inicialmente, apresenta-se uma simetria. Temos:
f(-2) = f(2) = 4
f(-1) = f(1) = 1
De um modo geral,
f(-x) = (-x)2 = x2 = f(x)
isto é, para todo x temos
f(-x) = f(x)
x | y = x2 | (x; y) |
-3 | 9 | (-3; 9) |
-2 | 4 | (-2; 4) |
-1 | 1 | (-1; 1) |
0 | 0 | (0; 0) |
1 | 1 | (1; 1) |
2 | 4 | (2; 4) |
3 | 9 | (3; 9) |
A curva obtida se chama parábola e toda equação quadrática y = a x2 + b x + c tem uma parábola como gráfico. O domínio da função é o conjunto dos números reais e seu conjunto imagem depende dos valores de a, b e c. Para a função f(x) = x2 o conjunto imagem é constituído por todos y 0.
Uma propriedade importante dessa parábola é que ela é simétrica em relação a uma reta vertical que se chama eixo de simetria. O gráfico da equação y = x2 é simétrico em relação ao eixo-y. Essa simetria deve-se ao fato de que f(-x) = (-x)2 = x2 = f(x) e que, portanto, a função é par.
A parábola tem um ponto de retorno, que se chama vértice. O vértice é a intersecção da parábola com o eixo de simetria.
No gráfico da equação y = x2 o vértice tem coordenadas (0; 0) e o valor mínimo da função é 0.
Note que, avançando da esquerda para a direita, a curva "desce" até a origem e depois "sobe". Dizemos que f é decrescente e que f é crescente.
f(x) = x2 é decrescente para x | f(x) = x2 é crescente para x |
f é crescente sobre o intervalo I se f(x1) < f(x2) sempre que x1 < x2, em I
f é decrescente sobre o intervalo I se f(x1) > f(x2) sempre que x1 < x2, em I
Exemplo.
Para a função f cujo gráfico está na figura, temos:
intervalo | crescimento/decrescimento |
x -2 x | f decresce f cresce f decresce |
Podemos usar o gráfico da equação y = x2 para construirmos os gráficos de outras funções quadráticas. Por exemplo, os gráficos das funções y = x2 + 1 e y = x2 - 1 podem ser obtidos do gráfico da equação y = x2 por translações verticais desse gráfico.
O gráfico de y = x2 + 1 é obtido deslocando o gráfico de y = x2 + 1 unidade para cima.
O gráfico de y = x2 -1 é obtido deslocando o gráfico de y = x2 1 unidade para baixo.
Também, podemos construir os gráficos das funções y = (x - 1)2 e y = (x + 1)2 a partir do gráfico de y = x2, fazendo translações horizontais desse gráfico.
O gráfico de y = (x - 1)2 é obtido deslocando o gráfico de y = x2 1 unidade para direita. O vértice está em (1;0) e o eixo de simetria é a reta x = 1.
O gráfico de y = (x + 1)2 é obtido deslocando o gráfico de y = x2 uma unidade para a esquerda. O vértice está em (-1;0) e o eixo de simetria é a reta x = - 1.
Nos gráficos que construímos até aqui, o coeficiente de x2 é 1. Se o coeficiente é -1, o efeito sobre o gráfico é uma reflexão em relação ao eixo-x.
Então, para a função y = - x2 o domínio continua sendo o conjunto dos números reais, mas o conjunto imagem é o conjunto dos números reais y tais que y 0.
O vértice está em (0; 0) e 0 é valor máximo da função.
x | y = - x2 | (x; y) |
-3 | -9 | (-3; -9) |
-2 | -4 | (-2; -4) |
-1 | -1 | (-1; -1) |
0 | 0 | (0; 0) |
1 | -1 | (1; -1) |
2 | -4 | (2; -4) |
3 | -9 | (3; -9) |
O gráfico de y = - x2 é obtido por reflexão do gráfico de y = x2 em torno do eixo-x.
Vimos que o gráfico de y = x2 tem um ponto de retorno no vértice; ele se dobra "para cima". Dizemos que a curva tem concavidade para cima. O gráfico de y = - x2 se dobra para baixo; dizemos que a curva tem concavidade para baixo.
Quando o coeficiente a em y = a x2 é diferente de 1, o gráfico dessa função pode ser obtido multiplicando a ordenada y, dos pontos de y = x2, pelo número a, como nos exemplos abaixo.
Cada ordenada é a metade da ordenada do gráfico de y = x2.
Cada ordenada é o dobro da ordenada do gráfico de y = x2.
Note que o gráfico de y = 2 x2 está "mais levantado" em relação ao gráfico de y = x2; o gráfico de y = 2 x2 "se afasta" do eixo-x. O gráfico de y = x2 "se aproxima" do eixo-x.
Exercícios.
1. Desenhar o gráfico da função y = - x2 + 3. Dizer onde a função é crescente ou decrescente. Qual é o conjunto-imagem da função?
Resolução
Partimos do gráfico de y = - x2; deslocando-o de 3 unidades "para cima", obtemos o gráfico de y = - x2 + 3.
A função y = - x2 + 3 é crescente para x ≤ 0 e é decrescente para x ≥ 0. Seu conjunto-imagem é constituído por todos y tais que y ≤ 3.
2. Desenhar o gráfico da função y = f(x) = (x + 2)2 - 2.
Resolução
Partimos do gráfico da função y = x2. Deslocando-o "para a esquerda" de 2 unidades, obtemos o gráfico de y = (x + 2)2; depois, deslocando-o "para baixo" de 2 unidades, obtemos o gráfico de y = f(x) = (x + 2)2 - 2.
Note que o conjunto-imagem da função f é constituído por todos y tais que y -2.
3. Desenhar o gráfico da parábola y = 2 (x - 2)2 + 1.
Resolução
Começamos com o gráfico de y = 2 x2; deslocando-o 2 unidades "para a direita", obtemos o gráfico de y = 2 (x - 2)2.
Então, deslocando-o 1 unidade "para cima" obtemos o gráfico de y = 2 (x - 2)2 = 1.
RAÍZES.
Para encontrar as raízes da função quadrática, conhecidas também como zero da função, é necessário o domínio das equações do segundo grau. Para resolver uma equação do segundo grau, há vários métodos, como a fórmula de Bhaskara e a soma e produto.
A raízes de uma função quadrática são os valores de x que fazem com que f(x) = 0. Sendo assim, para encontrar as raízes de uma equação do 2º grau, faremos ax² + bx + c = 0.
Exemplo:
f(x) = x² +2x – 3
a = 1
b = 2
c = –3
Δ =b² – 4ac
Δ=2² – 4 ·1·(-3)
Δ=4 +12
Δ = 16
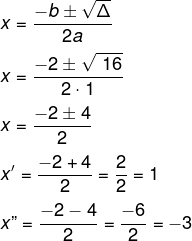
Então, os zeros da função são {1, -3}.
O valor do delta nos permite saber quantos zeros a função quadrática vai ter. Podemos separar em três casos:
- Δ > 0 → a função possui duas raízes reais distintas;
- Δ = 0 → a função possui uma única raiz real;
- Δ < 0 → a função não possui raiz real.
VÉRTICE.
O vértice da parábola corresponde ao ponto em que o gráfico de uma função do 2º grau muda de sentido. A função do segundo grau, também chamada de quadrática, é a função do tipo f(x) = ax2 + bx + c.
Usando um plano cartesiano, podemos traçar o gráfico de uma função quadrática considerando os pontos de coordenadas (x,y) que pertencem a função.
Na imagem abaixo, temos o gráfico da função f(x) = x2 - 2x - 1 e o ponto que representa seu vértice.
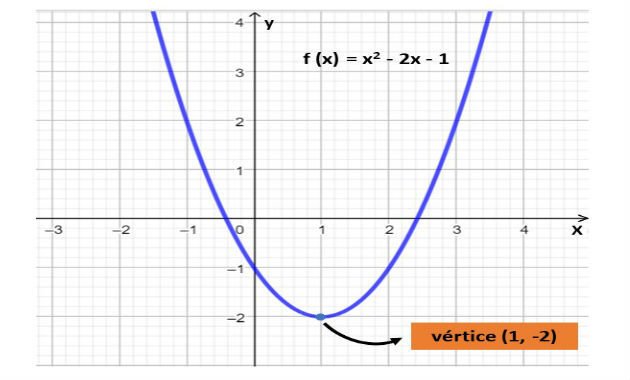
GRÁFICO DO GEOGEBRA.
Função Linear: observei que aparece no gráfico é uma função de cor verde, observo um ponto no eixo y, estão localizados na posição (0,1) onde, essa função é crescente pois a medida que o valor de x cresce o valor de y também cresce.
Função Quadrática: Uma parábola, Função Quadrática, Quando a é positivo, a parábola fica para cima. Quando a é negativo, a parábola fica para baixo. O gráfico vira uma reta coincidente ao eixo x, Quando a cresce, ele fecha, e quando a desce, ele abre, 1 (× ^ prime =B), 1 (x^ prime = B = V ). Quando a se aproxima de zero, o gráfico abre, quando a se afasta de zero, o gráfico fecha.
Nenhum comentário:
Postar um comentário